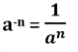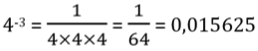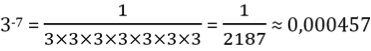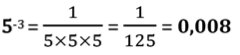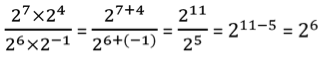3 000 ans avant notre ère, Belkib, roi des Indes, cherchait à tromper son ennui. Il promit donc une récompense exceptionnelle à qui lui proposerait une distraction. Lorsque le sage Sissa, lui présenta le jeu d'échecs, le souverain, enthousiaste, demanda à Sissa ce que celui-ci souhaitait en échange de ce cadeau extraordinaire. 
Humblement, Sissa demanda au roi de déposer un grain de riz sur la première case, deux sur la deuxième, quatre sur la troisième… et ainsi de suite pour remplir l'échiquier en doublant la quantité de riz à chaque case. 
Le prince accorda immédiatement cette récompense en apparence modeste… mais son conseiller lui expliqua qu'il venait de précipiter le royaume dans la ruine, car les récoltes de l'année ne suffiraient pas à payer Sissa. 

Les puissances

Grâce aux puissances, nous pouvons expliquer la fin de cette histoire.

Une puissance correspond à une multiplication répétée.

Si a est un nombre et n un nombre entier positif, alors aⁿ représente le nombre a, multiplié par lui-même n fois.

Par exemple : 7³ = 7 × 7 × 7 = 343  et  3⁷ = 3 × 3 × 3 × 3 × 3 × 3 × 3 = 2 187.

Revenons à nos grains de riz : le roi doit déposer 1 grain sur la première case, puis 2 grains sur la deuxième, 4 grains (2²) sur la troisième, 8 grains (2³) sur la quatrième… 
En continuant ainsi, il faudrait déposer 2⁶³ grains sur la dernière case, la 64^ème.  
2⁶³ = 2 × 2 × 2 × … × 2 = 9 223 372 036 854 775 808 grains, ce qui correspond à plus de 500 ans de la production mondiale actuelle de riz !

Quelques cas particuliers :

• tout nombre mis à la puissance 1 est égal à lui-même : 47¹ = 47
• tout nombre mis à la puissance 0 est toujours égal à 1 : 47  = 1. Même 0⁰ est égal à 1.

Une puissance peut être négative.

Si a est un nombre et n un nombre entier positif, alors 

C’est-à-dire que  

et 

Il faut faire bien attention à l’emplacement du signe –, qui n’a pas toujours la même signification :

 – 5³ = – 5 × 5 × 5 = – 125,

Mais 

Les formules utiles pour calculer les puissances

Pour effectuer des calculs avec des puissances, quelques formules sont à connaître: 

Multiplication et division

Si a est un nombre, et m et n des nombres entiers : 

Autrement dit, multiplier deux mêmes nombres avec des puissances revient à additionner les puissances, et diviser deux mêmes nombres avec des puissances revient à soustraire les puissances.

Ainsi, il peut être demandé d’écrire le calcul suivant avec une seule puissance 

 En utilisant les formules : 

Attention, ces formules ne fonctionnent qu’avec la multiplication et la division, mais pas avec l’addition et la soustraction. Par exemple, 3⁴ + 3⁵ n’est pas égal à 3⁹.

Puissance de puissance

Si a est un nombre, et m et n des nombres entiers :  (a^m)ⁿ = a^m×n 

Que se passe-t-il ? On met a à la puissance m, puis on remet le résultat à la puissance n. Cela revient à multiplier les puissances.

Par exemple, (11³)² donne le même résultat que 11⁶.

Nombres différents, même puissance

Si a et b sont des nombres, et n un nombre entier :  

Autrement dit, lorsqu’on multiplie deux nombres avec la même puissance, l’ordre dans lequel on effectue la multiplication et la mise à la puissance n’importe pas. Idem pour la division.

Attention, ces formules ne fonctionnent qu’avec la multiplication et la division, mais pas avec l’addition et la soustraction. Par exemple, 3² + 4² n’est pas égal à (3 + 4)².

La mise au carré (à la puissance 2) d’une addition ou d’une soustraction est étudiée en 3^ème grâce aux identités remarquables.

Les puissances de 10

Cette partie est en général déjà abordée en 4^ème, mais l’année de 3^ème peut être l’occasion d’un approfondissement.

Les puissances de 10 sont