Mathématiques
La réciproque du théorème de Pythagore en 4ème
Après l’étude du théorème de Pythagore vient l’étude de sa réciproque. Là où le théorème nous permet de calculer une longueur manquante dans un triangle rectangle, la réciproque a une toute autre utilité : démontrer qu’un triangle est bel et bien rectangle.
Énoncé
L’énoncé de la réciproque du théorème de Pythagore est le suivant :
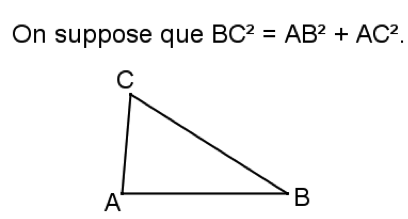
« Si dans un triangle ABC, on a BC² = AB² + AC², alors le triangle ABC est rectangle en A. »
C’est le théorème de Pythagore, lu à l’envers !
Vous vous demandez peut-être pourquoi on s’embête à étudier un énoncé qui ressemble beaucoup à celui du théorème. C’est tout simplement parce que si un énoncé est vrai, sa réciproque ne l’est pas forcément.
Considérons cette proposition, qui est vraie :
« Si un animal est un oiseau, alors il pond des œufs. »
Sa réciproque est :
« Si un animal pond des œufs, alors c’est un oiseau. »
Étant donné que d’autres animaux (notamment les poissons) pondent des œufs, la réciproque est fausse !
Dans le cas du théorème de Pythagore, il nous faut donc démontrer que la réciproque est bien vraie.
Démonstration de la réciproque du théorème de Pythagore
Comme nous l’avons fait pour le théorème, nous devons démontrer la réciproque suivante :
« Si dans un triangle ABC, on a BC² = AB² + AC², alors le triangle ABC est rectangle en A. »
Soit ABC un triangle vérifiant l’égalité BC² = AB² + AC².
On ne sait pas encore si un tel triangle est rectangle, c’est ce que nous allons chercher à démontrer.
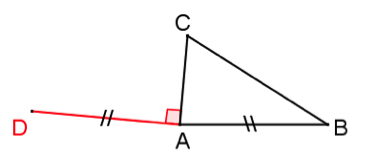
Nous pouvons, avec une équerre, tracer un segment [AD] de même longueur que [AB], perpendiculaire à AC et passant par A :
Ensuite, nous pouvons tracer [DC] pour obtenir le triangle ADC, qui par définition est rectangle.