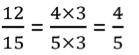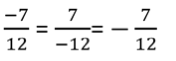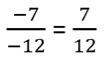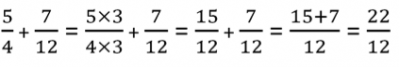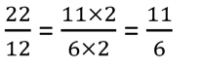Mathématiques
Les fractions en 4ème
Au collège, les fractions ne sont plus vues comme des simples « parts de gâteau ». Une fraction représente un quotient, c’est-à-dire le résultat d’une division.
En 5ème, on aborde généralement la simplification des fractions et les opérations entre fractions, notamment l’addition. En 4ème, d’autres possibilités s’ajoutent : les fractions peuvent comporter des nombres relatifs, et on découvre comment multiplier et diviser des fractions.
Simplification de fraction
Simplifier une fraction revient à l’écrire avec les plus petits nombres entiers possibles.
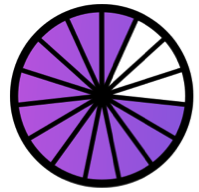
Par exemple, la fraction 12 ...... 15 peut se représenter par le partage ci-dessous :
Mais 12 et 15 sont divisibles par le même nombre : 3.
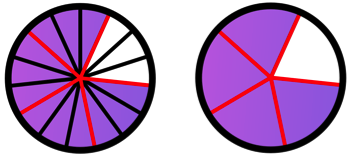
On peut donc les diviser par 3 tous les deux, sans changer la valeur de la fraction. Cela revient à faire un partage plus simple :
Il y a 3 fois moins de parts coloriées, mais également trois fois moins de part au total ! On passe de 12 parts sur 15 à 4 parts sur 5.
Cela se représente par le calcul suivant :
Nous avons donc simplifié la fraction en divisant son numérateur et son dénominateur par le même nombre : 3.
En 4ème, il arrive de devoir simplifier une fraction comportant des nombres négatifs.
- Si une fraction comporte un seul nombre négatif, alors elle est négative (d’après les règles de calcul sur les relatifs, le quotient de deux nombres de signe différent est négatif).
Ainsi, les trois fractions ci-dessous ont la même valeur :
On préfère placer le signe « moins » devant la fraction, comme dans la 3ème écriture.
- Si une fraction comporte deux nombres négatifs, alors elle est positive. On peut alors enlever les signes « moins ».
Addition et soustraction de fractions
En 5ème, on apprend qu’on ne peut pas ajouter ou soustraire n’importe quelles fractions. Il faut d’abord les réduire au même dénominateur.
Ainsi, pour calculer 5 .... 4 + 7 ...... 12 on remarque que 12 est un multiple de 4, c’est 4 × 3.
On reprend alors le calcul en multipliant le numérateur et le dénominateur de 5 .... 4 par 3 :
Pour terminer, on simplifie la fraction : 22 et 12 sont multiples de 2, donc :
En 4ème, on reprend ces opérations avec des nombres négatifs.
Calculons -3 ...... 2 - 9 .... 5 .
Il faut d’abord réduire les deux fractions au même dénominateur. Cela semble plus difficile, car 5 n’est pas multiple de 2.
La solution est de multiplier le numérateur et le dénominateur de -3 ...... 2 par 5, et le numérateur et le dénominateur de 9 .... 5 par 2. Ainsi, les deux dénominateurs seront identiques, et égaux à 2 × 5 !