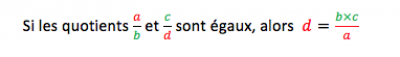La proportionnalité

On dit de deux grandeurs qu’elles sont proportionnelles lorsqu’on peut obtenir les valeurs de l’une en multipliant les valeurs de l’autre par un même nombre (qu’on appelle alors coefficient de proportionnalité).

Voici quelques exemples de grandeurs proportionnelles :

• lors d’une vente de fruits et légumes au poids, le prix est proportionnel à la masse de fruits achetés, et le coefficient est le prix au kilo.
• lorsqu’un véhicule roule à une vitesse constante, la distance parcourue (en km) est proportionnelle au temps (en h), le coefficient de proportionnalité est la vitesse (d’où les formules  et surtout  )

Quelques contre-exemples :

• la taille d’une personne n’est pas proportionnelle à son âge
• lors d’une vente de fruits et légumes à la pièce, le prix n’est plus proportionnel à la masse

Lorsqu’on dispose de deux grandeurs proportionnelles, on les représente souvent dans un tableau de proportionnalité :

Le coefficient de proportionnalité, qui permet de passer de la 1^ère ligne à la 2^ème par multiplication, est 123. En effet, 246 ÷ 2 = 123.

Ici, puisqu’il s’agit d’un tableau de distance proportionnelle au temps, ce coefficient correspond à la vitesse en km.h^-1. La vitesse est abordée en détail dans la fiche sur les grandeurs composées.

Votre enfant a probablement déjà appris de nombreuses méthodes pour compléter ces tableaux. Nous y reviendrons plus tard !

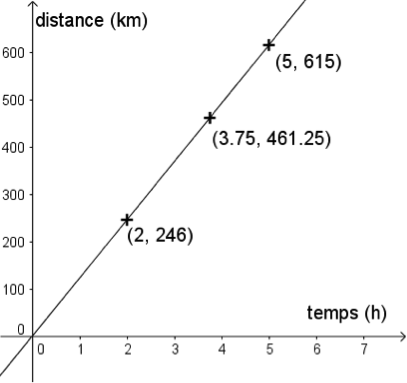
Deux grandeurs peuvent aussi se représenter dans un repère, chaque point correspondant à une colonne du tableau.

Dans une situation de proportionnalité, les points sont alors alignés avec l’origine du repère.

Rappel sur les quotients égaux

Autre notion importante mais déjà connue en début de 4^ème : la définition d’un quotient.

Le quotient d’un nombre a par un nombre b est le nombre noté :

a ÷ b ou  a .... b , tel que b x  a .... b  = a 

Autrement dit, un quotient, c’est tout simplement le résultat d’une division.

En général, les quotients se notent à l’aide d’une fraction à la place du symbole ÷.

Quelques exemples de quotients 

12 ...... 4  = 12 ÷ 4 = 3 (car 3 x 4 = 12). 

45 ...... 6  = 45 ÷ 6 = 7,5. 

10 ...... 3  ≈ 3,333333...

 Il existe des divisions qui « ne se terminent pas » et dont on ne peut pas écrire le quotient sous forme d’un nombre décimal. C’est le cas de  10 ...... 3  

 Il arrive que certains quotients soient égaux, c’est-à-dire que le résultat des divisions correspondantes sont identiques.

 Par exemple, voici plusieurs quotients égaux à 7,5 :  45 ...... 6  =  30 ...... 4  =  75 ...... 10  =  10,5 .......... 7  ... 

Et c’est en fait le sujet principal de cette partie du programme ! Nous allons maintenant voir :

• comment reconnaître des quotients égaux,
• comment s’en servir pour compléter des égalités ou résoudre des problèmes de proportionnalité.

Produit en croix et règle de trois

Pour savoir si des quotients sont égaux, il n’est pas toujours possible de faire la division correspondante !

Par exemple, les quotients  3 .... 7  et  4286 ............ 10001  

sont tous les deux à peu près égaux à 0,428… mais quand on poursuit la division, on se rend compte que l’un est à peu près égal à 0,42857 et l’autre à 0,42856, donc on ne peut pas dire qu’ils soient égaux ! 

Votre enfant a déjà vu une méthode pour « passer d’un quotient à un autre » :

La valeur d’un quotient ne change pas lorsqu’on multiplie ou divise le numérateur et le dénominateur par le même nombre.

Par exemple,  3 .... 4  est égal à  21 ...... 28  car   3 .... 4  =  3x7 ........ 4x7  =   21 ...... 28

De même,  45 ...... 6  est égal à  15 ...... 2  car  45 ...... 6  =  15x3 .......... 2x3  =  15 ...... 2

Passer de  45 ...... 6  à  15 ...... 2   s’appelle une simplification, cette technique est abordée avec plus de détails dans la fiche sur les fractions.

L’égalité des produits en croix

Il existe une autre propriété pour savoir si deux quotients sont égaux : l’égalité des produits en croix.

Si a, b, c et d sont des nombres (b et d étant non nuls), alors :

Des exercices d'applications