Spé Maths 1re
Fonctions dérivées, dérivées des fonctions usuelles
Des images en pèle pour expliquer une partie importante du programme de 1ère.
Après avoir découvert les nombres dérivés d’une fonction, nous sommes capables de déterminer si à un endroit donné, une fonction est croissante ou décroissante.
Ainsi, on peut calculer les nombres dérivés de la fonction f(x) = x3 – 2x² – x + 3 en plusieurs points :
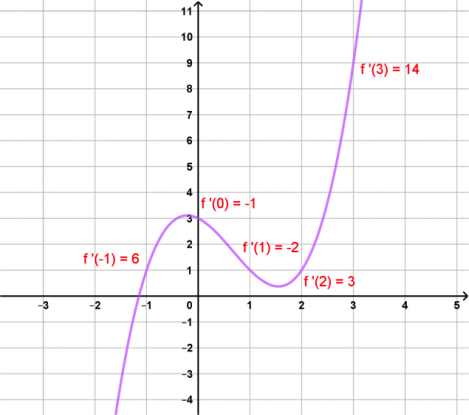
Courbe et nombres dérivés
La courbe de la fonction f, avec les nombres dérivés en -1, 0, 1, 2 et 3.
Ils sont positifs là où la fonction croît (en -1, 2 et 3), et négatifs sinon (en 0 et 1).
On peut donc calculer les nombres dérivés, les f’(x), pour tout x où la fonction est définie. Ce faisant, on définit une nouvelle fonction, associée à f : la fonction dérivée. On la note f’.
On verra plus tard (avec les dérivées des fonctions usuelles et les opérations sur les dérivées) que la fonction dérivée de f(x) = x3 – 2x² – x + 3 est f’(x) = 3x² – 4x + 1.
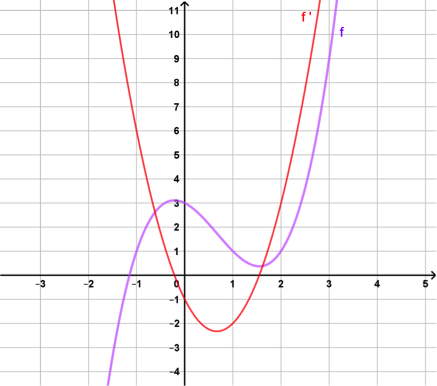
Traçons-les toutes les deux :
Relation entre fonction et dérivée
L’intérêt de cette fonction dérivée provient de celui du nombre dérivé.
On a vu que :
- si le nombre dérivé est positif, la fonction croît,
- si le nombre dérivé est négatif, la fonction décroît.
De plus, plus le nombre dérivé est grand, plus la fonction croît « vite ».
De même :
- si la fonction dérivée est positive, la fonction croît,
- si la fonction dérivée est négative, la fonction décroît.
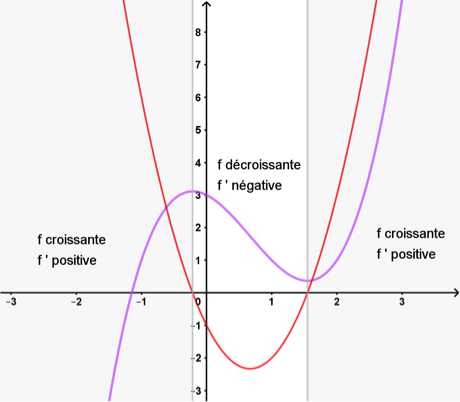
Signe de la dérivée et variation
Ainsi, les fonctions dérivées sont très utiles pour étudier le sens de variation (croissant ou décroissant) d’une fonction.
Comment trouver les fonctions dérivées ?
La lecture est réservée à nos abonnés
- Prolongez votre lecture pour 1€ Acheter cette fiche
- Abonnez-vous à partir de 4€/mois Découvrir nos offres