Spé Maths 1re
Les limites de suite
L’étude des limites permet de mieux comprendre comment les phénomènes étudiés évolueront avec le temps.
Les suites permettent, comme nous avons vu dans le cours sur les suites, de modéliser des phénomènes « discrets » : évolution d’une population, d’un compte bancaire…
Quand on étudie les suites, on voit que les valeurs de certaines d’entre elles se rapprochent de plus en plus d’un nombre donné.
Ce nombre sera alors appelé « limite » de la suite.
Quelques exemples de limites de suite
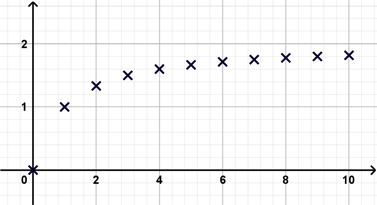
Prenons la suite un = 1 ........ n+1
On a u = 1 ; u1 = 0,5 ; u2 ≈ 0,333 ; u3 = 0,25 , etc.
En représentant cela dans un repère, on obtient ceci :
Suite qui tend vers 0
Les valeurs prises par la suite se rapprochent de plus de plus de 0.
On dit que la limite de la suite (un) est 0, ou que la suite « tend » ou « converge » vers 0 quand n tend vers + ∞.
On le note ainsi : limn+∞ 1 ........ n+1 = 0
ce qui se lit « la limite de 1 ........ n+1 quand n tend vers + ∞ est 0 ».
Étudions maintenant vn = 2n ........ n+1
Suite qui tend vers 2
Les valeurs de la suite se rapprochent de plus en plus de 2.
On notera alors limn+∞ 2n ........ n+1 = 2
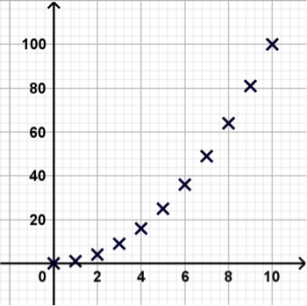
Regardons wn = n2
Suite divergente vers l’infini
Les valeurs de cette suite ne se rapprochent pas d’un même nombre, mais continuent de croître de plus en plus vite.
On dit que la suite « diverge vers + ∞ » ou « tend vers + ∞ » et on note limn+∞ n2 = + ∞
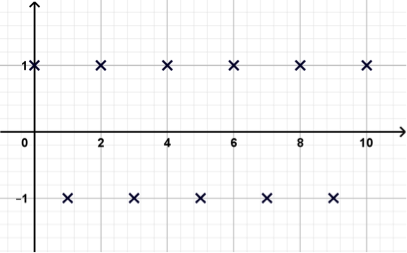
Considérons an = (-1)n
Suite divergente
C’est une suite un peu particulière, qui prend les valeurs 1 et -1 alternativement.
Ses valeurs ne se rapprochent donc pas d’un même nombre, puisqu’elles continueront d’alterner entre 1 et -1. On dit alors que « la suite (an) diverge ».
Dans une autre fiche, on a vu les suites géométriques !
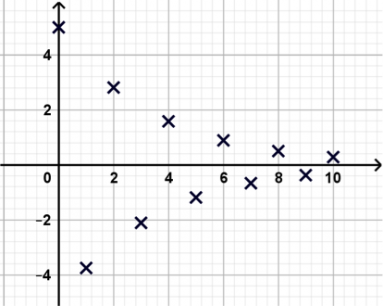
Regardons la suite géométrique (bn) de premier terme 5 et de raison -0,75. On a alors pour n entier positif : bn = 5 × (-0,75)n.
Suite qui tend vers 0
Les valeurs de la suite sont, comme ci-dessus, alternativement positives et négatives, mais se rapprochent tout de même de 0.
Donc lim n+∞ bn = 0
Ce n’est pas le cas pour toutes les suites géométriques. Nous allons maintenant voir comment calculer les limites des suites plus rigoureusement.
Calculer une limite
La lecture est réservée à nos abonnés
- Prolongez votre lecture pour 1€ Acheter cette fiche
- Abonnez-vous à partir de 4€/mois Découvrir nos offres