Spé Maths 1re
Opérations sur les dérivées
Une fois la notion de nombre dérivé et les dérivées des fonctions usuelles connues, on calcule les dérivées de toutes les autres fonctions à partir des fonctions usuelles, en effectuant des opérations. C’est ce que nous allons voir dans cette fiche !
Multiplications par une constante
On commence par le cas le plus simple.
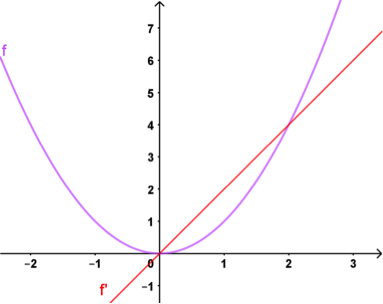
Partons d’une fonction f dérivable, comme par exemple f(x) = x² et sa dérivée f’(x) = 2x :
Fonction et dérivée
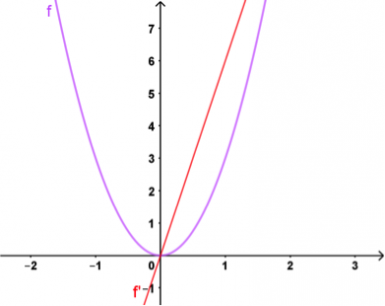
Si on multiplie les valeurs de cette fonction par un nombre constant, par exemple 3 pour obtenir f(x) = 3x², il est clair que la fonction croîtra ou décroîtra 3 fois plus « vite » :
Autre dérivée
La dérivée de la fonction f(x) = 3x² est donc f’(x) = 3 × 2x = 6x.
Plus généralement :
Si on multiplie une fonction par un nombre constant k, sa dérivée sera multipliée par ce nombre k.
Autrement dit : la dérivée de k × f est k × f’.
On peut le démontrer avec la définition du nombre dérivé par les limites, comme vu dans la fiche sur les fonctions dérivées.
Petit exemple : quelle est la dérivée de f(x) = 7x4 ?
On sait que la dérivée de g(x) = x4 est g’(x) = 4x3, donc la dérivée de f est f’(x) = 7 × 4x3 = 28x3.
Additions et soustractions
La lecture est réservée à nos abonnés
- Prolongez votre lecture pour 1€ Acheter cette fiche
- Abonnez-vous à partir de 4€/mois Découvrir nos offres