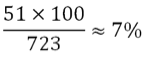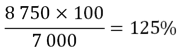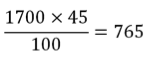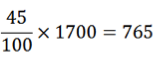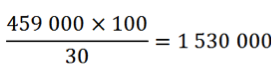Mathématiques
Les pourcentages en 3ème
L’année de 3ème est l’occasion de consolider les connaissances sur la proportionnalité, et d’étudier des techniques plus efficaces pour calculer des augmentations ou des diminutions de pourcentage (ce qui s’avère bien pratique pour les soldes !).
Les pourcentages permettent d’étudier une proportion en la ramenant à une fraction de 100.
Il est en effet plus simple de dire « environ 34% des électeurs ont voté pour un candidat » plutôt que « 23 118 électeurs sur 68119 ont voté pour un candidat »!
Mathématiquement, un pourcentage peut être vu comme une fraction de dénominateur 100 : 37% = 37 ........ 100 .
Calculer un pourcentage
« Dans une usine, on a testé 723 pièces. 51 pièces étaient défectueuses. Quel est le pourcentage de pièces défectueuses ? »
Il s’agit de résoudre ce problème de proportionnalité :
Les 723 correspondent à la totalité des pièces, c’est pourquoi dans le tableau, on les fait correspondre aux 100%.
On applique ensuite la règle de trois :
pour trouver qu’environ 7% des pièces sont défectueuses.
Il arrive, lors d’une augmentation, d’obtenir des pourcentages supérieurs à 100%.
Ainsi, si le prix d’une voiture passe de 7 000€ à 8 750€, on calcule ce que représente le nouveau prix par rapport à l’ancien :
On effectue le calcul suivant :
Le nouveau prix représente 125% de l’ancien. On dit aussi que le prix a augmenté de 25%.
Appliquer un pourcentage
« Lors d’une élection municipale où 1700 suffrages ont été recueillis, 45% des votants ont choisi le candidat le plus jeune. Combien de votants ont choisi ce candidat ? »
Il s’agit de résoudre ce problème :
On applique la règle de trois :
Ainsi, 765 votants ont choisi le candidat le plus jeune.
Ce problème revient à prendre une fraction d’un nombre.
Ici, on aurait pu multiplier la fraction 45 ........ 100 , qui représente 45%, par le nombre 1 700 :
On trouve le même résultat sans utiliser la proportionnalité.
Retrouver une valeur
« Lors d’une élection régionale, le candidat le plus jeune a recueilli 459 000 voix au premier tour, ce qui représente 30% des suffrages exprimés. Combien y avait-il de suffrages exprimés ? »
C’est le problème inverse du précédent :
On applique la règle de trois :
Ainsi, il y avait 1 530 000 suffrages exprimés.