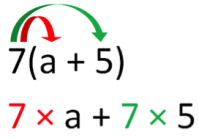C’est une partie assez abstraite du programme de mathématiques en collège, mais indispensable à plus haut niveau ! La distributivité est une application du calcul littéral qui permet de transformer une somme en un produit (factoriser), ou l’inverse (développer). 

Retrouvez ici les formules de distributivité et des liens vers des sites pour s'entraîner. 

Développer 

Développer un produit, c’est le transformer en une somme.

Avec la distributivité, développer revient à passer de « k(a + b) » à « ka + kb ».

En général, on ne le fait qu’avec des expressions littérales : on n’a pas besoin de développer pour calculer des produits comme 15 × (7 + 11), qu’on pouvait déjà calculer avant d’entendre parler de distributivité.

Il existe tout de même quelques techniques pour calculer des produits difficiles de tête, à l’aide de nombres « ronds », et de la distributivité. 
Ces techniques sont plutôt étudiées en 5^ème.

Par exemple, pour calculer 8 × 39, on remplace 39 par (40 – 1), ce qui nous donne 8 × (40 – 1), puis en développant : 

8 × (40 – 1)
= 8 × 40 – 8 × 1
= 320 – 8
= 312.

Intéressons-nous maintenant à ce qui se passe lorsque le produit contient une lettre.

Développons 7(a + 5) :

7(a + 5)
= 7 × a + 7 × 5       (on applique la distributivité)
= 7a + 35                (7 × a peut s’écrire 7a, et 7 × 5 font 35).
Et c’est tout : on ne peut pas calculer 7a + 35, car on ne connaît pas la valeur de a.

Vous étiez prévenus en début de fiche : c’est abstrait.

On a juste dit que « 7(a+ 5) » pouvait s’écrire « 7a + 35 ». 
Dans un premier temps, il n’y a pas beaucoup d’applications concrètes. Mais il faut étudier les développements avant de passer à d’autres choses, comme se servir de la distributivité pour démontrer des propriétés, ou résoudre des équations.

Notez qu’il est possible, lorsqu’on débute, de dessiner des flèches sur l’expression à développer, pour montrer qu’on distribue le facteur commun aux deux termes de la parenthèse, comme ci-dessous :

Il y a plusieurs petites difficultés à prendre en compte :

Développons y(6 – x) 

y(6 – x)
= y × 6 – y × x         
= 6y - yx                 

Développons (n – 11) × n 

(n – 11) × n
n(n – 11)                 
(on est plus habitués à l’écrire dans ce sens, sans le signe ×)
= n × n – n × 11    
= n² - 11n             

Développons -5(a – 3) 

-5(a – 3)                  
= -5 × a – (-5) × 3                     
(attention, il y a deux signes – : celui de -5 et celui de la soustraction a – 3)
= -5a + 5 × 3                             
(soustraire un nombre revient à ajouter son opposé : on transforme  –(-5) en +5)
= -5a + 15

Développement double